Derivative of Ln X

To find the derivative of secant we could either use the limit definition of the derivative which would take a very long time or the definition of secant itself. F x lnx f x 1 x.

Finding The Derivative Of F X Ln Ln Lnx Using The Chain Rule Math Videos Calculus Chain Rule

1st Derivative Test If x c is a critical point of fx then x c is 1.

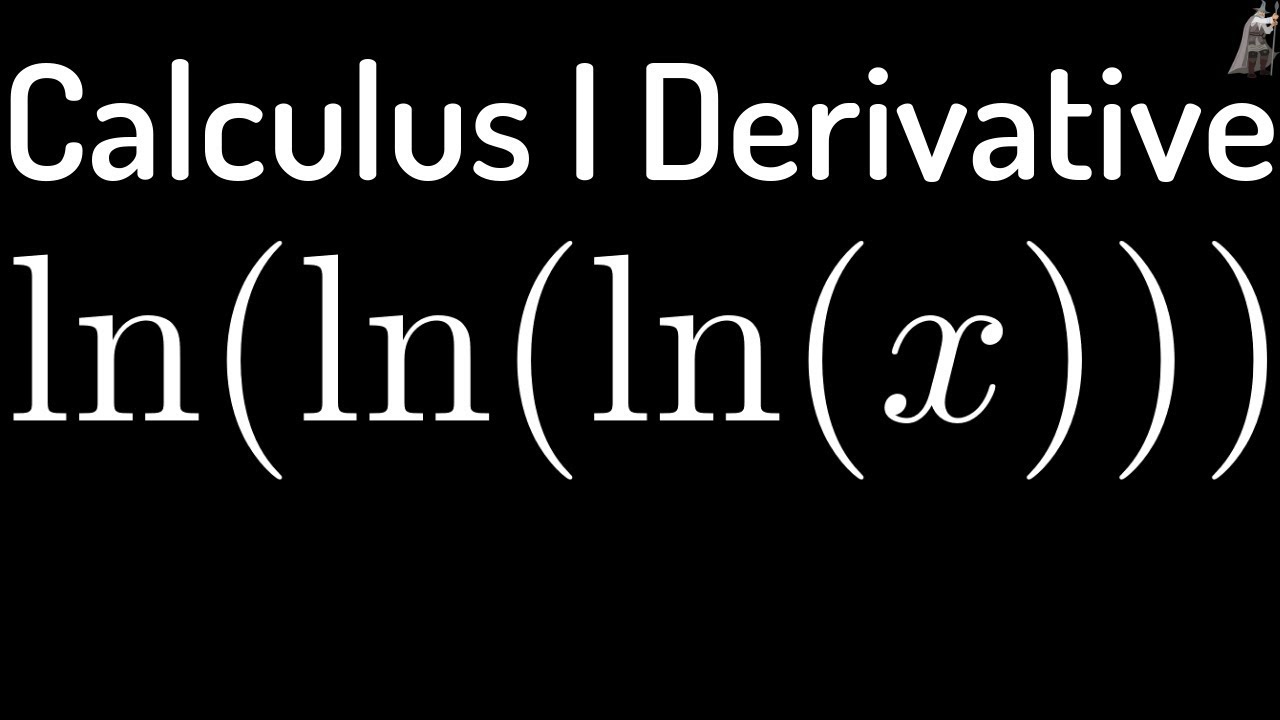
. Ln0 is undefined. Lets start with simple example. D dx lnfx fx fx 2x x 2 5 3The final answer is d dx lnx 2 5 2x x 2 5.

2 Now lets take fx fx and plug them into the derivative rule. The second derivative of e-x is just itself. A ln d xx dx x a Calculus Cheat Sheet.

This formula list includes derivatives for constant trigonometric functions polynomials hyperbolic logarithmic. Taking natural logarithm with base e of both sides we get that. Relative to a hyperreal extension R R of the real numbers the derivative of a real function y fx at a real point x can be defined as the shadow of the quotient y x for infinitesimal x where y fx x.

Solve d dw log e 4w. You also have the option to plot another function in green beneath that calculated slope. Ln of negative number.

In the context described where A -A are both real and the log used is standard Ln-1 is undefined. So to find the second derivative of e-x we just need to differentiate -e-x. Secx1cosx We know ddxcosx-sinx - keep that in mind because were going to need it.

Lnxdx x lnx - 1 C. The known derivatives of the elementary functions x 2 x 4 sinx lnx and expx e x as well as the constant 7 were also used. A Differentiation formulas list has been provided here for students so that they can refer to these to solve problems based on differential equations.

2nd Derivative Test If x c is a critical point of fx such. We can use the chain rule to calculate the derivative of -e-x and get an answer of e-x ie. Begingroup Well calling Ln-1 iPi is already expanding the standard definition of Ln.

Lim lnx when x. Ln-1 iπ Logarithm product rule. So lets say that f of x is equal to the natural log of x.

Integration goes the other way. A logarithm is the opposite of a powerIn other words if we take a logarithm of a number we undo an exponentiation. But Id say the intelligent thing is to break it into two undefined improper integrals with one of the limits at 0 where it is unbounded.

The given equation is a square root function 81. The Derivative tells us the slope of a function at any point. Lim lnx when x.

Then f prime of x is equal to 1 over x. The slope of a line like 2x is 2 or 3x is 3 etc. Ln of negative number.

In differential calculus we learned that the derivative of lnx is 1x. It plots your function in blue and plots the slope of the function on the graph below in red by calculating the difference between each point in the original function so it does not know the formula for the derivative. This is one of the most important topics in higher class Mathematics.

The solution is quite simple. To calculate the second derivative of a function you just differentiate the first derivative. Ln y 12 ln x.

Free derivative calculator - differentiate functions with all the steps. However if x is negative then lnx is undefined. Find the derivative of y 81.

Ln0 is undefined. Lnx is undefined when x 0. Derivative of Root x by Logarithmic Differentiation.

The Second Derivative of ex2. The general representation of the derivative is ddx. There are rules we can follow to find many derivatives.

If you were to take the derivative of it its 1 over x. So good candidate for f of x is natural log of x. The natural logarithm of a number is its logarithm to the base of the mathematical constant e which is an irrational and transcendental number approximately equal to 2718 281 828 459The natural logarithm of x is generally written as ln x log e x or sometimes if the base e is implicit simply log x.

Ln1 0. Here are useful rules to help you work out the derivatives of many functions with examples belowNote. Derivative of a Constant Raised to the X Power.

We can use the chain rule in combination with the product rule for differentiation to calculate the derivative. The antiderivative of 1x is lnx. Lnxdx x lnx - 1 C.

Lnx is undefined when x 0. From above we found that the first derivative of ex2 2xe x 2So to find the second derivative of ex2 we just need to differentiate 2xe x 2. Of fx if fx 0 to the left of x c and fx 0 to the right of x c.

The natural logarithm is usually written lnx or log e x. Fxcthenf0x0 Constant Multiple Rule. The derivative of the natural logarithm function is the reciprocal function.

From above we found that the first derivative of e-x -e-x. Differentiating with respect to x we have frac1y fracdydx frac12 cdot. The natural log is the inverse function of the exponential function.

If the lines coincide there is a good chance you have found the derivative. Ln1 0. Type in any function derivative to get the solution steps and graph.

And lets set g. Of fx if fx 0 to the left of x cand fx 0to the right of x c. Now we will find the derivative of x with the help of the logarithmic derivative.

The integral or antiderivative of 1x should be a function whose derivative is 1x. Not a relative extrema of fx if fx is the same sign on both sides of x c. Remember that a square root is a number multiplied by it to get the resulting number.

Ddxsecx Since secx1cosx we can write this as. The logarithm of the multiplication of x and y is the sum of logarithm of x. Y x 12.

Let me write this down. F x lnx f x 1 x. 2 x 2 x ln 2 Therefore the derivative of 2 x is 2 x ln2.

The second derivative of e-x e-x. Derivative of natural logarithm ln function. Related Pages Natural Logarithm Logarithmic Functions Derivative Rules Calculus Lessons.

Derivative of a Square Root Function. As we just saw this is lnx. Note that frac11xsum_n ge 0 -1nxn Integrating both sides gives you beginalign ln1x sum_n ge 0frac-1nxn1n1 x-fracx2.

And for g prime of x you want to find something where its easy to take the antiderivative of it. The slope of a constant value like 3 is always 0. Natural Log ln The Natural Log is the logarithm to the base e where e is an irrational constant approximately equal to 2718281828.

Taking the derivative of that gives us fx 2x. Parentheses are sometimes added for clarity giving lnx log e x or logx. The little mark means derivative of and.

How To Find The Derivative Of F X Ln X 3 1 Using The Chain Rule Chain Rule Math Videos F X

Derivative Of F X Sqrt Ln X Math Videos Calculus F X

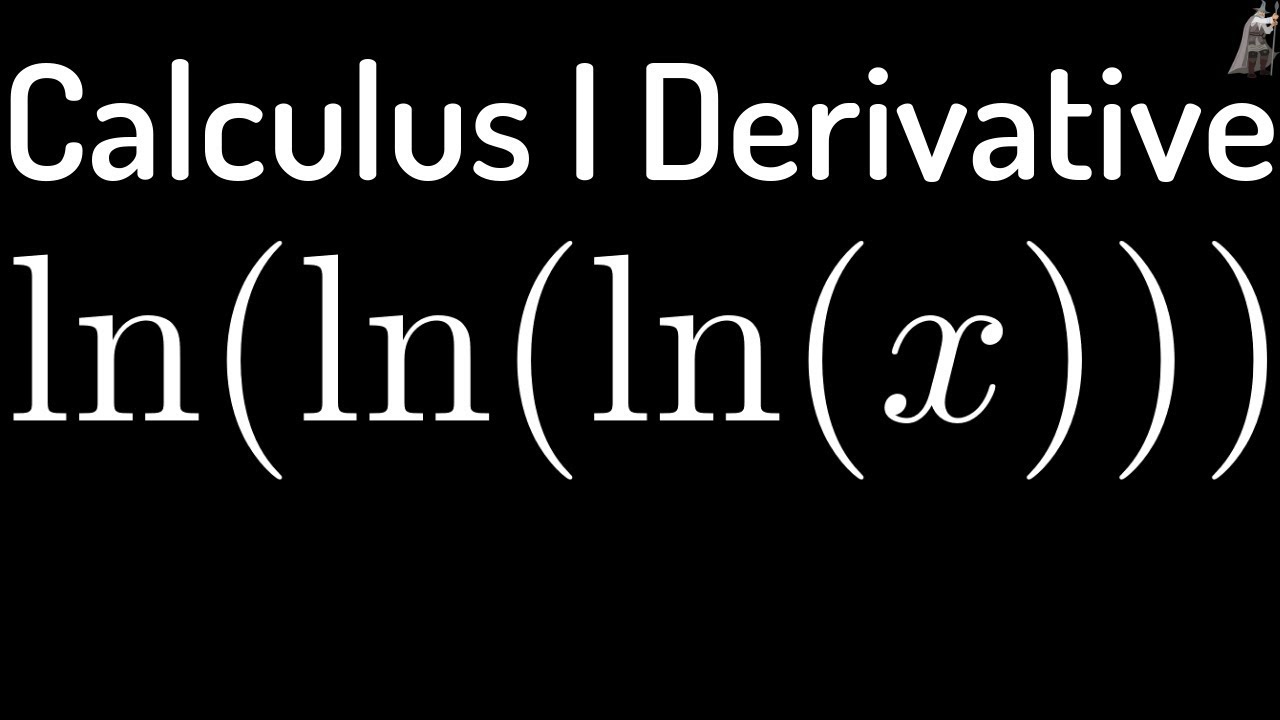
Finding The Derivative Of F X Ln Ln Lnx Using The Chain Rule Math Videos Calculus Chain Rule

Derivation Of The Derivative Of Ln X Using Limits D Dx Ln X 1 X Proof Rigorous Calculus Ab Bc For More Cool Math Videos Visit M Calculus Math Videos Fun Math